Το Πρόβλημα του Fagnano (GeoGebra)

Στις πλευρές ενός οξυγώνιου τριγώνου ABC να βρεθούν τρία σημεία D,E,F διαφορετικά από τις κορυφές του, τέτοια ώστε η περίμετρος του τριγώνου DEF να είναι ελάχιστη.

Λύση.
Δείτε και επεξεργαστείτε το σχήμα της λύσης σε GeoGebra.

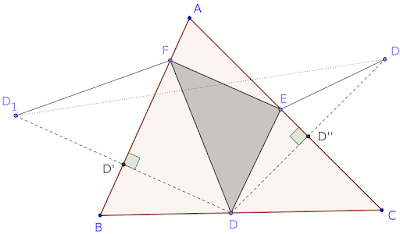
Έστω $DEF$ ένα τυχαίο τρίγωνο εγγεγραμμένο στο $ABC$. Θέλουμε να προσδιορίσουμε τη θέση των σημείων $D,E,F$ έτσι ώστε το άθεοισμα $DE+EF+FD$ να είναι ελάχιστο.

Έστω $D_1$ και $D_2$ τα συμμετρικά του $D$ ως προς τις πλευρές $AB$ και $AC$ αντίστοιχα. Τότε $FD=FD_1$ και $ED=ED_2$ από ισότητα των τριγώνων $FD'D_1,FD'D$ και $DED'',D''ED$. Δηλαδή η περίμετρος του τριγώνου $DEF$ ισούται με το μήκος της τεθλασμένης γραμμής $D_1 FED_2$. Γνωρίζουμε όμως ότι από όλες τις τεθλασμένες γραμμές με άκρα τα $D_1$ και $D_2$,  ελάχιστο μήκος έχει το $D_1 D_2$.

Σύμφωνα με τα παραπάνω μπορούμε να λύσουμς το παρακάτω ειδικό πρόβλημα:

Από όλα τα εγγεγραμμένα τρίγωνα στο $ABC$ με κορυφή ένα τυχαίο σημείο $D$ της πλευράς $BC$, την ελάχιστη περίμετρο έχει το τρίγωνο $DFE$, όπου $F$ και $E$ τα σημεία τομής της $D_1D_2$ με τις $AB,AC$ αντίστοιχα. Η περίμετρος αυτού του τριγώνου είναι ίση με το μήκος του ευθύγραμμου τμήματος $D_1D_2$.

Άρα για την λύση του προβλήματος θα πρέπει να προσδιορίσουμε για ποιά θέση του $D$ πάνω στη $BC$ το μήκος $D_1D_2$ είναι ελάχιστο. Παρατηρούμε ότι:

$$AD_1=AD=AD_2\ \ \text{και}\ \ \hat{D_1AD_2}=2\hat{A}.$$

Δηλαδή το τρίγωνο $AD_1D_2$ είναι ισοσκελές και έχει σταθερή τη γωνία της κορυφής. Επομένως η βάση του $D_1D_2$ θα γίνει ελάχιστη όταν γίνει ελάχιστο το μήκος των ίσων πλευρών, δηλαδή το μήκος $AD$. Αυτό όμως συμβαίνει όταν το $AD$ είναι κάθετο στην $BC$. Άρα η θέση του $D$ που ελαχιστοποιεί την περίμετρο του τριγώνου $DEF$  είναι το ίχνος του ύψουςαπό την κορυφή $A$ στην πλευρά $BC$.

Επειδή αντί του $D$ θα μπορούσαμε να είχαμε χρησιμοποιήσει το σημείο $E$ ή $F$ καταλήγουμε στο επόμενο συμπέρασμα που είναι και η λύση του προβλήματος:

Από όλα τα εγγεγραμμένα τρίγωνα στο οξυγώνιο τρίγωνο $ABC$ την ελάχιστη περίμετρο έχει εκείνο με κορυφές τα ίχνη των υψών του $ABC$ πάνω στις πλευρές.

Το τρίγωνο αυτό ονομάζεται ορθικό τρίγωνο του $ABC$.

Tweet

Posted in: Γεωμετρία,Τρίγωνο,Geogebra